Procédurier - Utiliser R en mesure et évaluation

##############################################################################
## Fichier: CLAS_exos_01a.r date: juillet 2007
## Auteur: AndréSèb Aubin ()
##
## Dans ce script (Les numéros de page font référence à l'ouvrage de Bertrand et Blais)
## Exercices du chapitre 2 (pages 63 à 65)
## - numéro 1
## - numéro 3
## - numéro 5
## - numéro 9
## - numéro 15
##############################################################################


##############################################################################
##############################################################################
##############################################################################
## Exercice chapitre 02 - numéro 1 (p.63)
## Objectifs:

exerc_2.1 <- matrix(0,7,2)

# Pour cet exercice nous entrerons à la main les valeurs dans la matrice

exerc_2.1 <- edit(exerc_2.1) # permet d'éditer le contenu de la matrice exerc_2.1

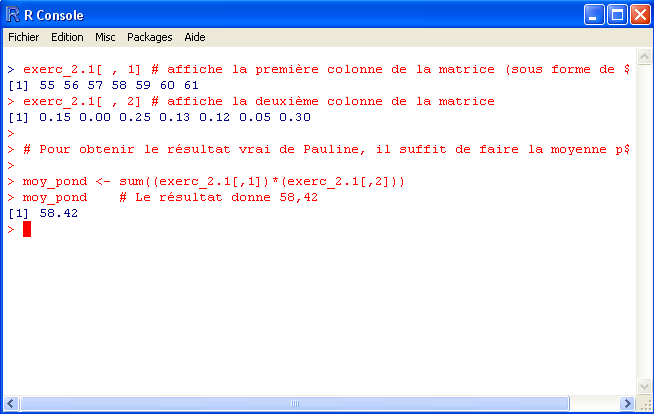
exerc_2.1[ , 1] # affiche la première colonne de la matrice (sous forme de ligne)
exerc_2.1[ , 2] # affiche la deuxième colonne de la matrice

# Pour obtenir le résultat vrai de Pauline, il suffit de faire la moyenne pondérée

moy_pond <- sum((exerc_2.1[,1])*(exerc_2.1[,2]))
moy_pond # Le résultat donne 58,42

##############################################################################
##############################################################################
##############################################################################
## Exercice chapitre 02 - numéro 3 (p.63)
## Objectifs: L'objectif est de trouvé deux échantillons (A et B) dont alpha_A sera
## plus grand que alpha_B et dont sd_A sera plus petit que sd_B
## Rappelons qu'il est nécessaire de charger la librairie psy pour accéder
## au calcul de alpha
## Rappelons aussi que la fonction sd() permet de calculer l'écart-type.

library(psy)

## Nous allons procéder par une génération aléatoire d'un échantillon A, puis nous allons
## générer plusieurs échantillons B, jusqu'au moment où nous obtiendrons un échantillon B
## répondant aux deux conditions.

## Génération d'un échantillon A (pour l'exercice, fixons un échantillons de 10 items
## (0 ou 1) et de 100 individus)

matrice_A <- matrix(0,100,10)
# matrice_A #désactivé pour réduire l'affichage dans la Console R

# Pour chaque élément de cette matrice, nous choisirons un 0 ou un 1 au hasard

i <- 0 # initialisation de la variable des lignes
for (i in 1:100)
{
j <- 0 # initialisation de la variable des colonnes
for (j in 1:10)
{
t <- as.integer(runif(1)*2)
matrice_A[i,j] <- t
}
}
# edit(matrice_A) désactivé pour réduire l'affichage dans la Console R
matrice_resul_A <- rowSums(matrice_A)

moyenne_A <- mean(matrice_resul_A)
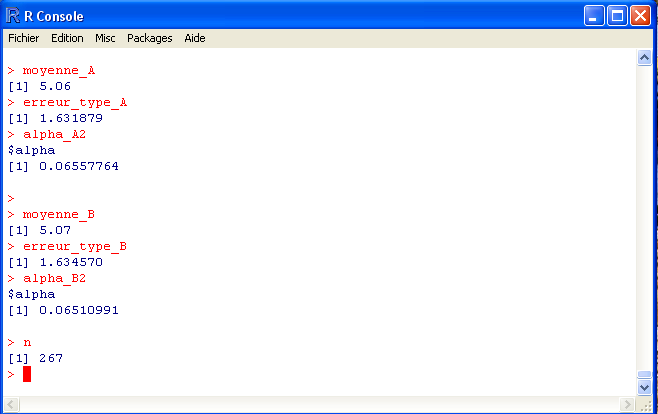
moyenne_A
erreur_type_A <- sd(matrice_resul_A)
erreur_type_A
alpha_A <- cronbach(matrice_A)
alpha_A2 = alpha_A[3]

# Générons maintenant un échantillon B (de la même taille, bien que ce ne soit pas spécifié).
matrice_B <- matrix(0,100,10)

test <- 0 # variable d'arrêt de la boucle (arrêt quand test == 'OK')
n <- 0
while(test != 'OK')
{

k <- 0 # initialisation de la variable des lignes
for (k in 1:100)
{
l <- 0 # initialisation de la variable des colonnes
for (l in 1:10)
{
u <- as.integer(runif(1)*2)
matrice_B[k,l] <- u
}
}

## edit(matrice_B) désactivé pour réduire l'affichage dans la Console R
matrice_resul_B <- rowSums(matrice_B)

moyenne_B <- mean(matrice_resul_B)
moyenne_B
erreur_type_B <- sd(matrice_resul_B)
erreur_type_B
alpha_B <- cronbach(matrice_B)
alpha_B
alpha_B2 = alpha_B[3]

if ((erreur_type_B > erreur_type_A))
{
if ((alpha_A$alpha > alpha_B$alpha))
{
test <- 'OK' # si les deux conditions sont vrais, alors test = OK FIN de la boucle
}
}

n <- n+1
}

moyenne_A
erreur_type_A
alpha_A2

moyenne_B
erreur_type_B
alpha_B2
n # nombre d'essais nécessaires pour obtenir une matrice B répondant aux conditions.

##############################################################################
##############################################################################
##############################################################################
## Exercice chapitre 02 - numéro 5 (p.63)
## Objectifs: Dans ce cas-ci, la génération aléatoire ne semble pas appropriée,
## puisqu'il s'agit de cas très spécifiques où les 2 coefficients de bissection,
## le coefficient de Cronbah et L2 donnent 1

# Reprenons le format du tableau 2.7
C2_ex_05 <- matrix(0, 16,8)
C2_ex_05 <- edit(C2_ex_05)

alpha_C2_5 <- cronbach(C2_ex_05)
alpha_C2_5