

style1
Section 05 - Chapitre 07 - L'analyse factorielle
Les boîtes de Thurstone
Pour notre premier exemple d'analyse factorielle, nous utiliserons un cas classique d'introduction.
Le script pour cette page est disponible en cliquant ici.
## Dans la présent script nous travaillerons sur l'analyse factorielle à
## partir d'un exemple plutôt scolaire.
## Il s'agit du problème des 20 boîtes de Thurstone qui permet de
## s'initier à la mécanique de l'analyse factorielle.
## Il s'agit d'un exemple construit pour mieux comprendre l'analyse factorielle.
## En partant d'un échantillon constitué de 20 boîtes dont la largeur,
## la longueur et la hauteur varient, nous tenterons de retrouver ces trois éléments.
## Cependant, comme dans un vrai problème, nous n'avons pas accès
## à ces 3 facteurs de base, mais d'une matrice que nous fabriquerons avec
## les valeurs du logarithme (log), de la mise au carré (^2) et de l'exponentielle e (exp).
# Pour obtenir les valeurs de départ des boîtes.
t7.1a <- read.table("http://pages.usherbrooke.ca/asaubin/r_project/data/donnees_7_1a_TBP.data")
t7.1a
## partir d'un exemple plutôt scolaire.
## Il s'agit du problème des 20 boîtes de Thurstone qui permet de
## s'initier à la mécanique de l'analyse factorielle.
## Il s'agit d'un exemple construit pour mieux comprendre l'analyse factorielle.
## En partant d'un échantillon constitué de 20 boîtes dont la largeur,
## la longueur et la hauteur varient, nous tenterons de retrouver ces trois éléments.
## Cependant, comme dans un vrai problème, nous n'avons pas accès
## à ces 3 facteurs de base, mais d'une matrice que nous fabriquerons avec
## les valeurs du logarithme (log), de la mise au carré (^2) et de l'exponentielle e (exp).
# Pour obtenir les valeurs de départ des boîtes.

## Pour créer la matrice x^2 exp(x) et log(x)
deux_t7.1a = t7.1a * t7.1a
deux_t7.1a
exp_t7.1a = exp(t7.1a)
exp_t7.1a
log_t7.1a = lg(t7.1a)
log_t7.1a
## La fonction cbind() permet d'associer les colonnes (contrairement à rbind() pour les lignes)
## La matrice finale est t7.1_full
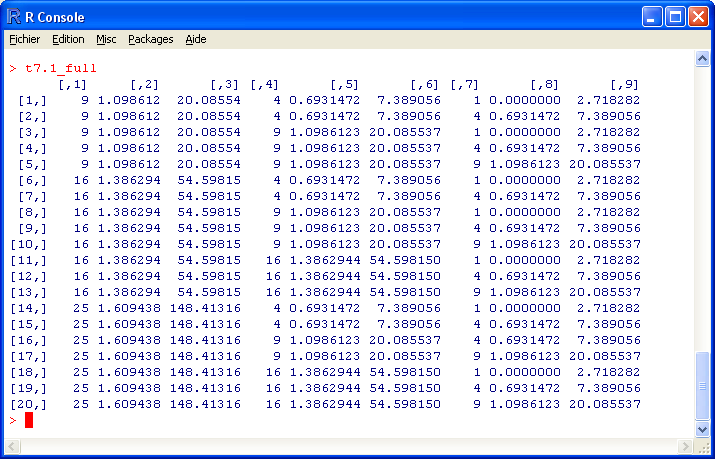
t7.1_full <- cbind(deux_t7.1a[,1], log_t7.1a[,1], exp_t7.1a[,1], deux_t7.1a[,2], log_t7.1a[,2], exp_t7.1a[,2], deux_t7.1a[,3], log_t7.1a[,3], exp_t7.1a[,3])
## La fonction cbind() permet d'associer les colonnes (contrairement à rbind() pour les lignes)
## La matrice finale est t7.1_full
## L'ANALYSE FACTORIELLE - Première méthode
## Les prochaines étapes seront réalisées sur la matrice X,
## permettant plus de polyvalence du script.
## L'objectif de l'analyse factorielle est de réduire un ensemble de données ## en un plus petit nombre de facteurs. Ce regroupement permettra de simplifier
## le travail sur les données et d'assurer une meilleure compréhension de celles-ci.
## Évidemment, le nombre maximum de facteurs possibles est le nombre total de variables.
## X contient les 9 colonnes de données de base et donc, nous tenterons de réduire ce nombre.
## Dans notre exemple, qui est un cas pour mieux comprendre, notre matrice contient des
## informations sur 9 variables pour 20 sujets. Le nombre maximal de facteurs est donc 9.
## Mais, vu qu'il s'agit d'un exemple construit, nous savons que nous cherchons à atteindre
## 3 facteurs (dans notre cas la largeur, la longueur et la hauteur des boîtes.
X <- t7.1_full
X
## Première étape, trouvons la matrice de corrélations de notre matrice de données X.
CX <- cor(X)
## Trouvons ensuite la valeurs des vecteurs propres de la matrice CX
ECX <- eigen(CX)
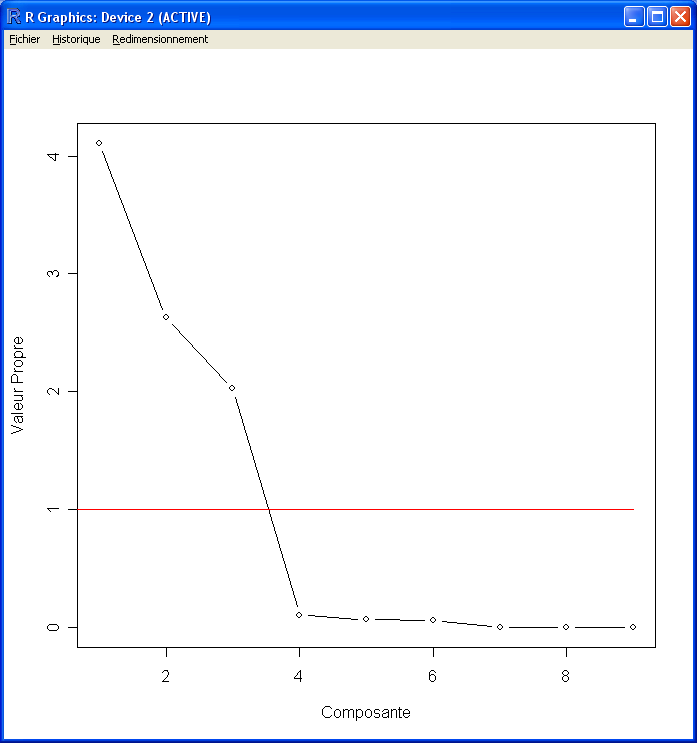
## Dans le cas de l'analyse factorielle, la représentation graphique est souvent intéressante.
plot(eigen(CX)$values, type="b", xlab="Composante", ylab="Valeur Propre")
lines(x=c(0,9),y=c(1,1), col="red")
## Les prochaines étapes seront réalisées sur la matrice X,
## permettant plus de polyvalence du script.
## L'objectif de l'analyse factorielle est de réduire un ensemble de données ## en un plus petit nombre de facteurs. Ce regroupement permettra de simplifier
## le travail sur les données et d'assurer une meilleure compréhension de celles-ci.
## Évidemment, le nombre maximum de facteurs possibles est le nombre total de variables.
## X contient les 9 colonnes de données de base et donc, nous tenterons de réduire ce nombre.
## Dans notre exemple, qui est un cas pour mieux comprendre, notre matrice contient des
## informations sur 9 variables pour 20 sujets. Le nombre maximal de facteurs est donc 9.
## Mais, vu qu'il s'agit d'un exemple construit, nous savons que nous cherchons à atteindre
## 3 facteurs (dans notre cas la largeur, la longueur et la hauteur des boîtes.
## Première étape, trouvons la matrice de corrélations de notre matrice de données X.
## Trouvons ensuite la valeurs des vecteurs propres de la matrice CX
## Dans le cas de l'analyse factorielle, la représentation graphique est souvent intéressante.
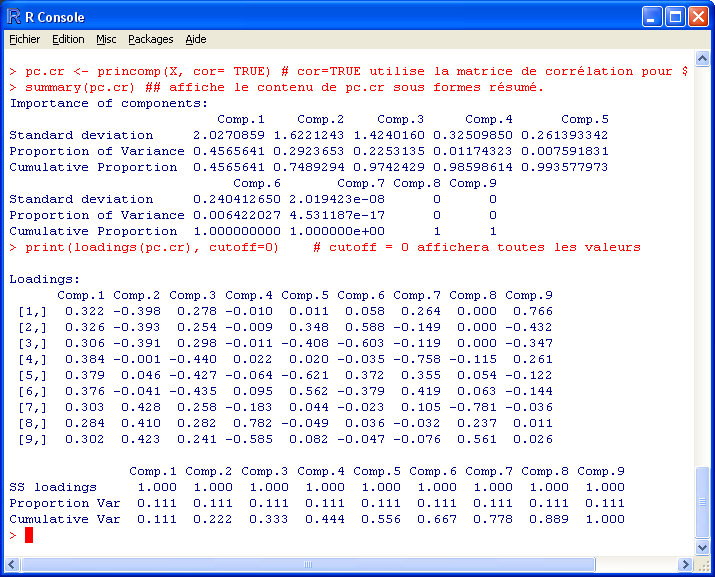
## Certaines fonctions de l'environnement R nous permettent d'accélérer l'obtention des
## facteurs. La fonctions princomp() retourne l'analyse des composante.
## Pour apercevoir le contenu de notre matrice en enlevant les entrées trop petites
## il est possible de modifier la valeur de cutoff.

## La fonction plot(pc.cr) permet d'afficher le diagramme des éboulis.
## À partir de ce diagramme, il est possible d'extraire les facteurs en observant
## le changement dans la pente du graphique.
plot(pc.cr) # affiche le graphique des éboulis.
## À partir de ce diagramme, il est possible d'extraire les facteurs en observant
## le changement dans la pente du graphique.


Cela complète ce premier exemple.
Dernière mise à jour faite le 21 janvier 2017 à 13:10 -0800 par
| 
|