##############################################################################
## Auteur: AndréSèb Aubin
##
## Dans ce script
## - Ogive normale
## - Modèle de Rasch
## - Modèle à un paramètre
## - Modèle à deux paramètres
## - Modèle à trois paramètres
## - +quation d'information maximale à trois paramètres

##############################################################################

## Theta est égal de -3 à 3

Theta = seq(-3, 3, by=0.1)
Theta


##############################################################################
##############################################################################
## Ogive normale (approximation de Birnbaum)

## Valeur des paramètres
D = 1.7
ai = 1
bi = 0

Pi_norm <- 0
Pi_norm = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_norm

plot(Theta, Pi_norm, type="l")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)

##############################################################################
##############################################################################
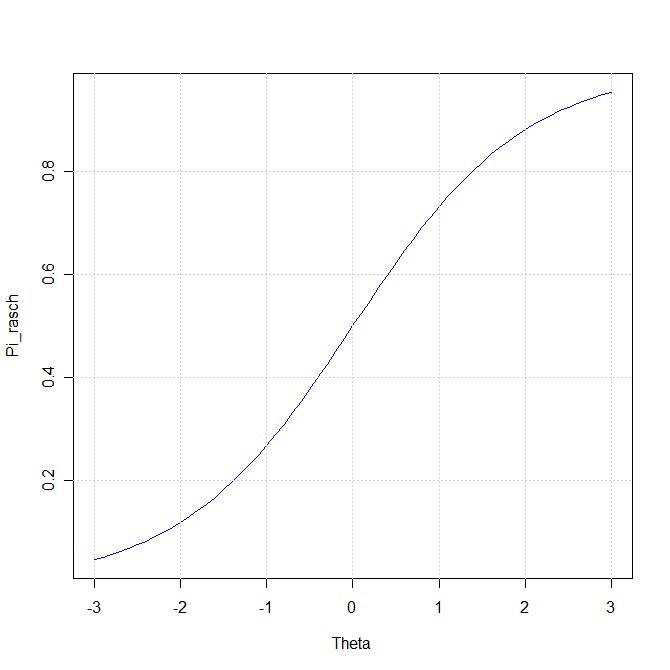
## Modèle de Rasch

D = 1 # fixe dans le modèle de Rasch
ai = 1 # fixe dans le modèle de Rasch
bi = 0 # varie dans le modèle de Rasch selon d'indice de difficulté

Pi_rasch <- 0
Pi_rasch = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_rasch

plot(Theta, Pi_rasch, type="l", col="blue")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)

###############################################################################
###############################################################################
## Modèle à un paramètre

D = 1.7 # fixe dans le modèle à un paramètre
ai = 1 # fixe dans le modèle à un paramètre
bi = 0 # varie dans le modèle à un paramètre selon d'indice de difficulté

Pi_1p <- 0
Pi_1p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_1p

plot(Theta, Pi_1p, type="l", col="red")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

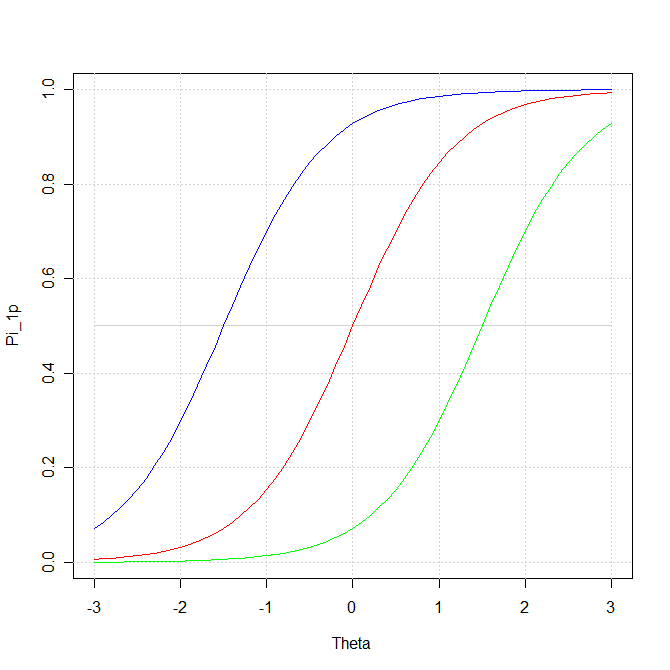
## Reproduisons la figure 4.18 (page 128)
bi = -1.5
Pi_1p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_1p
lines(Theta, Pi_1p, type="l", col="blue")

bi = 0
Pi_1p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_1p
lines(Theta, Pi_1p, type="l", col="red")

bi = 1.5
Pi_1p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_1p
lines(Theta, Pi_1p, type="l", col="green")

###############################################################################
###############################################################################
## Modèle à deux paramètres

D = 1.7 # fixe dans le modèle à deux paramètre
ai = 1 # varie dans le modèle à deux paramètre
bi = 0 # varie dans le modèle à deux paramètres

Pi_2p <- 0
Pi_2p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_2p

lines(Theta, Pi_2p, col="yellow")

## Reproduisons la figure 4.20 (page 130)
plot(Theta, Pi_2p, type="l", col="lightgray")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

bi = 0
ai = 2
Pi_2p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_2p
lines(Theta, Pi_2p, type="l", col="blue")

bi = 0
ai = 0.5
Pi_2p = 1/(1+exp(-D*ai*(Theta-bi)))
Pi_2p
lines(Theta, Pi_2p, type="l", col="red")

## Pour connaître la valeur exacte de la fonction à un Theta spécifique

Pi_2p[which(Theta == 0)] # Valeur de Pi_2p quand Theta = 0

> Pi_2p[which(Theta == 0)] # Valeur de Pi_2p quand Theta = 0
[1] 0.5

###############################################################################
###############################################################################
## Modèle à trois paramètres

D = 1.7 # fixe dans le modèle à trois paramètres
ai = 1 # varie dans le modèle à trois paramètres
bi = 0 # varie dans le modèle à trois paramètres
ci = 0 # varie dans le modèle à trois paramètres


Pi_3p <- 0
Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p

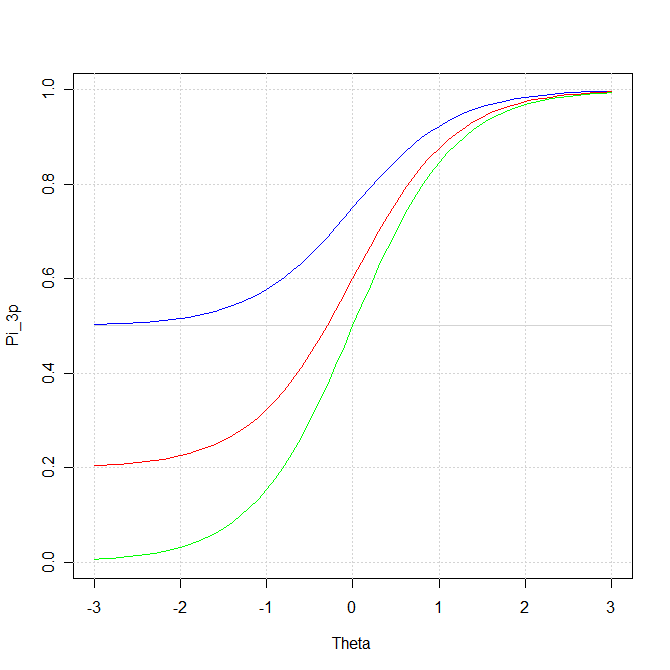
## Reproduisons la figure 4.23 (page 135)
plot(Theta, Pi_3p, type="l", col="lightgray")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

bi = 0
ai = 1
ci = 0.5

Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p
lines(Theta, Pi_3p, type="l", col="blue")

bi = 0
ai = 1
ci = 0.2

Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p
lines(Theta, Pi_3p, type="l", col="red")

bi = 0
ai = 1
ci = 0

Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p
lines(Theta, Pi_3p, type="l", col="green")

###############################################################################
###############################################################################
## Reproduction de la figure 4.25 à l'aide du modèle à 3 paramètres

# item 1
bi = 0
ai = 2
ci = 0.25

Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p1 = Pi_3p
plot(Theta, Pi_3p, type="l", col="green")

# item 2
bi = 0
ai = 2.5
ci = 0.3

Pi_3p = ci + (1-ci)/(1+exp(-D*ai*(Theta-bi)))
Pi_3p2 = Pi_3p
lines(Theta, Pi_3p, type="l", col="blue")

##############################################################################<br>
###############################################################################<br>
###############################################################################<br>
## Obtention de la courbe d'information maximale relative à l'item i <br>

# Réinitialisation des paramètres
bi = 0
ai = 1
ci = 0

## Pour le modèle à trois paramètres

Ii_max = (Dˆ2*aiˆ2)/(8*(1-ci)ˆ2) * (1 - 20*ci - 8*ciˆ2 + (1+8*ci)ˆ1.5)
Ii_max

## Pour le modèle à deux paramètres ci = 0 et donc

Ii_max = (Dˆ2*aiˆ2)/(8*(1)ˆ2) * (1 + (1)ˆ1.5)
Ii_max

## Pour le modèle à un paramètre ci = 0 et ai = 1 et donc

Ii_max = (Dˆ2)/(8*(1)ˆ2) * (1 + (1)ˆ1.5)
Ii_max
##############################################################################

> # Réinitialisation des paramètres
> bi = 0
> ai = 1
> ci = 0
>
## Pour le modèle à trois paramètres
>
> Ii_max = (Dˆ2*aiˆ2)/(8*(1-ci)ˆ2) * (1 - 20*ci - 8*ciˆ2 + (1+8*ci)ˆ1.5)
> Ii_max
[1] 0.7225
>
> ## Pour le modèle à deux paramètres ci = 0 et donc
>
> Ii_max = (Dˆ2*aiˆ2)/(8*(1)ˆ2) * (1 + (1)ˆ1.5)
> Ii_max
[1] 0.7225
>
> ## Pour le modèle à un paramètre ci = 0 et ai = 1 et donc
>
> Ii_max = (Dˆ2)/(8*(1)ˆ2) * (1 + (1)ˆ1.5)
> Ii_max
[1] 0.7225
> ##############################################################################