##############################################################################
## Auteur: AndréSèb Aubin
##
## Dans ce script
## - Exercices du chapitre 4 (pages 167 à 169)
## - numéro 2
## - numéro 4
## - numéro 5
## - numéro 7
## - numéro 8

##############################################################################

## Exercice chapitre 04 - numéro 2 (p.167)
## Objectifs: dessiner trois courbes d'item (1, 2 et 3) répondant au critères
## spécifiées.

## Nous utiliserons le modèle à deux paramètres, puisqu'il n'est pas question
## de pseudo-chance et donc ci = 0

Theta = seq(-3, 3, by=0.1) ## définition de Theta de -3 à 3

D = 1.7 # fixe dans le modèle à deux paramètres
ai = 1 # varie dans le modèle à deux paramètres * initialisation
bi = 0 # varie dans le modèle à deux paramètres * initialisation

Pi_2p <- 0

## item 1 (avec bi1) dessinons la courbe standard, comme point de départ.
bi1 = 0
ai1 = 1
Pi_2p1 = 1/(1+exp(-D*ai1*(Theta-bi1)))
Pi_2p1

plot(Theta, Pi_2p1, type="l", col="blue")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

## item 2 (avec bi2) * cette courbe doit être près de l'item 1

bi2 = -0.5
ai2 = 1
Pi_2p2 = 1/(1+exp(-D*ai2*(Theta-bi2)))
Pi_2p2

lines(Theta, Pi_2p2, type="l", col="red") # ajout sur le graphique déjà ouvert

## item 3 (avec bi3) * cet item est plus difficile que l'item 1 et 2

bi3 = 1
ai3 = 1
Pi_2p3 = 1/(1+exp(-D*ai3*(Theta-bi3)))
Pi_2p3

lines(Theta, Pi_2p3, type="l", col="green") # ajout sur le graphique déjà ouvert

## Pour vérifier, calculons le maximum de vraisamblance (ML) de chaque item

## Nuréro 02 + COMPL+TER##################################################################

################################################################################
################################################################################
## Exercice chapitre 04 - numéro 4 (p.167)
## Objectifs: Dessinez les courbes, puis répondre à la question
## Nous utiliserons le modèle à trois paramètres (ai, bi et ci)

Theta = seq(-3, 3, by=0.1) ## définition de Theta de -3 à 3

D = 1.7 # fixe dans le modèle à trois paramètres
ai = 1 # varie dans le modèle à trois paramètres * initialisation
bi = 0 # varie dans le modèle à trois paramètres * initialisation
ci = 0 # varien dans le modèle à trois paramètres * initialisation

Pi_3p <- 0

# item 1 (ai1 = 0.2; bi1 = 0 ; ci1 = 0)

ai1 = 0.2
bi1 = 0
ci1 = 0

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))

plot(Theta, Pi_3p1, type="l", col="red")
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

# item 2 (ai2 = 0.5; bi2 = 0.5 ; ci2 = 0)

ai2 = 0.5
bi2 = 0.5
ci2 = 0

Pi_3p2 = ci2 + (1-ci2)/(1+exp(-D*ai2*(Theta-bi2)))

lines(Theta, Pi_3p2, type="l", col="blue")

# item 3 (ai3 = 2; bi3 = -2 ; ci3 = 0.2)

ai3 = 2
bi3 = -2
ci3 = 0.2

Pi_3p3 = ci3 + (1-ci3)/(1+exp(-D*ai3*(Theta-bi3)))

lines(Theta, Pi_3p3, type="l", col="green")

################################################################################
################################################################################
## Exercice chapitre 04 - numéro 5 (p.168)
## Objectifs: Retrouver les caractéristiques de la courbe illustrée
## Nous utiliserons le modèle à trois paramètres (ai, bi et ci)

Theta = seq(-3, 3, by=0.1) ## définition de Theta de -3 à 3

D = 1.7 # fixe dans le modèle à trois paramètres
ai = 1 # varie dans le modèle à trois paramètres * initialisation
bi = 0 # varie dans le modèle à trois paramètres * initialisation
ci = 0 # varien dans le modèle à trois paramètres * initialisation

Pi_3p <- 0

## essai 1 (ai = 1; bi = 1.5 ; ci = 0.2)
## Nous savons que ci = 0.2 grÔce au minimum de la courbe
## et que bi = 1.5 grÔce à la situation du point d'inflexion
## ainsi...

ai1 = 1
bi1 = 1.5
ci1 = 0.2

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))

plot(Theta, Pi_3p1, type="l", col="red", xlim = range(-3, 3), ylim = range(0, 1))
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

# La pente est trop forte, réduisons la valeur de ai
# Essai 2

ai1 = 0.5
bi1 = 1.5
ci1 = 0.2

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))
lines(Theta, Pi_3p1, type="l", col="blue")

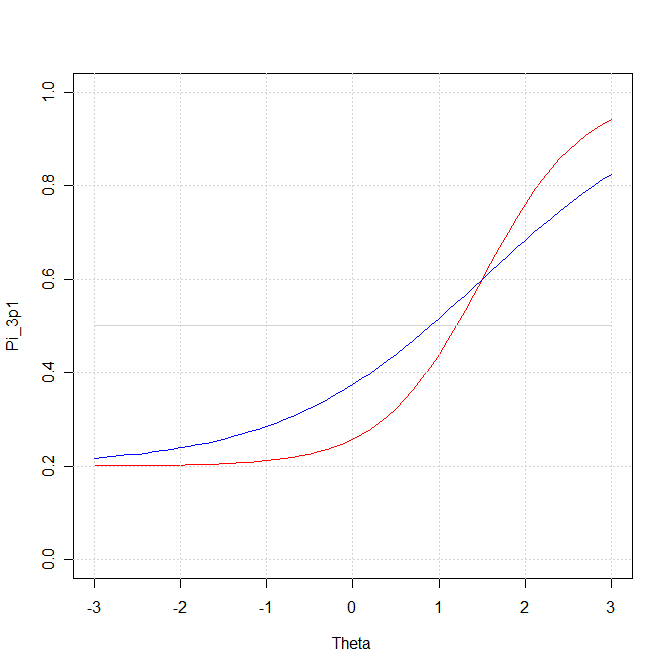
# La courbe est très près de celle illustrée, et ce malgré le fait que le solutionnaire donne une autre réponse.

################################################################################
################################################################################
## Exercice chapitre 04 - numéro 7 (p.168)
## Objectifs: Retrouver les caractéristiques de la courbe illustrée
## Nous utiliserons le modèle à trois paramètres (ai, bi et ci)

Theta = seq(-3, 3, by=0.1) ## définition de Theta de -3 à 3

D = 1.7 # fixe dans le modèle à trois paramètres
ai = 1 # varie dans le modèle à trois paramètres * initialisation
bi = 0 # varie dans le modèle à trois paramètres * initialisation
ci = 0 # varien dans le modèle à trois paramètres * initialisation

Pi_3p <- 0

## Essai 1 (ai = 0; bi = 0.5 ; ci = 0.6)
## Nous savons que ci = 0.6 grÔce au minimum de la courbe
## et que bi = 0.5 grÔce à la situation du point d'inflexion
## Pour ai, la pente est nulle donc ai = 0
## ainsi...

ai1 = 0
bi1 = 0.5
ci1 = 0.6

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))

plot(Theta, Pi_3p1, type="l", col="red", xlim = range(-3, 3), ylim = range(0, 1))
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

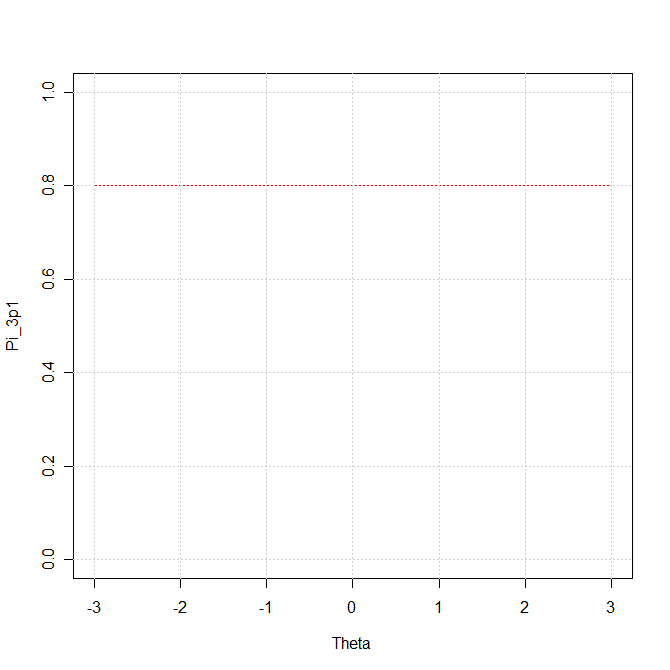
# La courbe a la bonne pente, mais elle n'est pas au bon endroit...
# Essai 2
# nous savons qu'à Theta = 0.5 -> Pi = 0.6
# alors que 0.6 = ci1 + (1-ci1)/(1 + exp(0))
# ainsi 0.6 = ci1 + (1-ci1)/2 et donc 1.2 = 2ci1 + 1 - ci1 -> ci1 = 0.2

ai1 = 0
bi1 = 0.5
ci1 = 0.2

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))
lines(Theta, Pi_3p1, type="l", col="blue")

# Cela correspond à la courbe de l'exercice 7


################################################################################
################################################################################
## Exercice chapitre 04 - numéro 8 (p.168)
## Objectifs: Reproduire la courbe et déterminer sa particularité
## Nous utiliserons le modèle à trois paramètres (ai, bi et ci)

Theta = seq(-3, 3, by=0.1) ## définition de Theta de -3 à 3

D = 1.7 # fixe dans le modèle à trois paramètres
ai = 1 # varie dans le modèle à trois paramètres * initialisation
bi = 0 # varie dans le modèle à trois paramètres * initialisation
ci = 0 # varien dans le modèle à trois paramètres * initialisation

Pi_3p <- 0

# Entrons les valeurs données dans l'équation

ai1 = -0.5
bi1 = 0
ci1 = 0.35

Pi_3p1 = ci1 + (1-ci1)/(1+exp(-D*ai1*(Theta-bi1)))

plot(Theta, Pi_3p1, type="l", col="red", xlim = range(-3, 3), ylim = range(0, 1))
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE)
lines(x = c(-3,3), y = c(0.5,0.5), col="lightgray")

# Cette courbe est descendante, ce qui signifie qu'elle est mieux réussie par les
# personne ayant un théta faible.