

style2
Procédurier - Utiliser R en mesure et évaluation
Section 09 C - Analyse du PISA2006 par l'analyse factorielle.
Voici la section où nous ferons une analyse factorielle en utilisant des scores associés aux mathématiques et aux sciences.
##=============================================================================
## Fichier: Section_09C_gamma.r date: juin 2009
## Auteur: AndréSèb Aubin (andreseb.aubin@gmail.com)
##
## Dans ce script
## Analyse de données du PISA2006 par l'analyse factorielle
##
## F_In: data1 (fait dans le script transtype_alpha.r)
## Vérification du nombre de facteurs
##
##=============================================================================
##=============================================================================
## 00 - N'oubliez pas de vous assurez que toutes les librairies sont chargées.
##=============================================================================
score_compil <- na.omit(data1)
View(score_compil)
write.table(score_compil, file="score_2006.dat", row.names=TRUE, col.names=TRUE, sep="\t")
X <- score_compil
## Première étape, trouvons la matrice de corrélations de notre matrice de données X.
CX <- cor(X)
## Trouvons ensuite la valeurs des vecteurs propres de la matrice CX
ECX <- eigen(CX)
## Dans le cas de l'analyse factorielle, la représentation graphique est souvent intéressante.
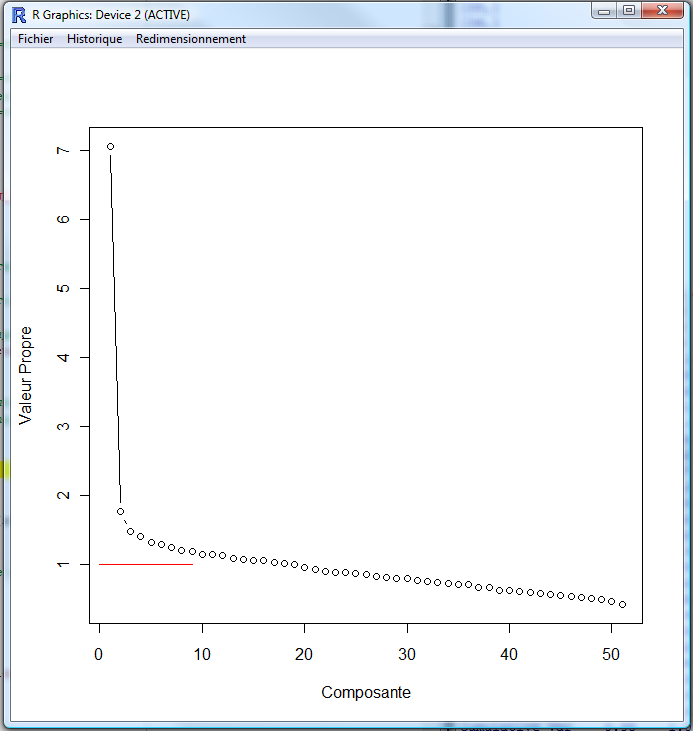
plot(eigen(CX)$values, type="b", xlab="Composante", ylab="Valeur Propre")
lines(x=c(0,9),y=c(1,1), col="red")
## Fichier: Section_09C_gamma.r date: juin 2009
## Auteur: AndréSèb Aubin (andreseb.aubin@gmail.com)
##
## Dans ce script
## Analyse de données du PISA2006 par l'analyse factorielle
##
## F_In: data1 (fait dans le script transtype_alpha.r)
## Vérification du nombre de facteurs
##
##=============================================================================
##=============================================================================
## 00 - N'oubliez pas de vous assurez que toutes les librairies sont chargées.
##=============================================================================
View(score_compil)
write.table(score_compil, file="score_2006.dat", row.names=TRUE, col.names=TRUE, sep="\t")
X <- score_compil
## Première étape, trouvons la matrice de corrélations de notre matrice de données X.
Voici le schéma résultant de cette première méthode.
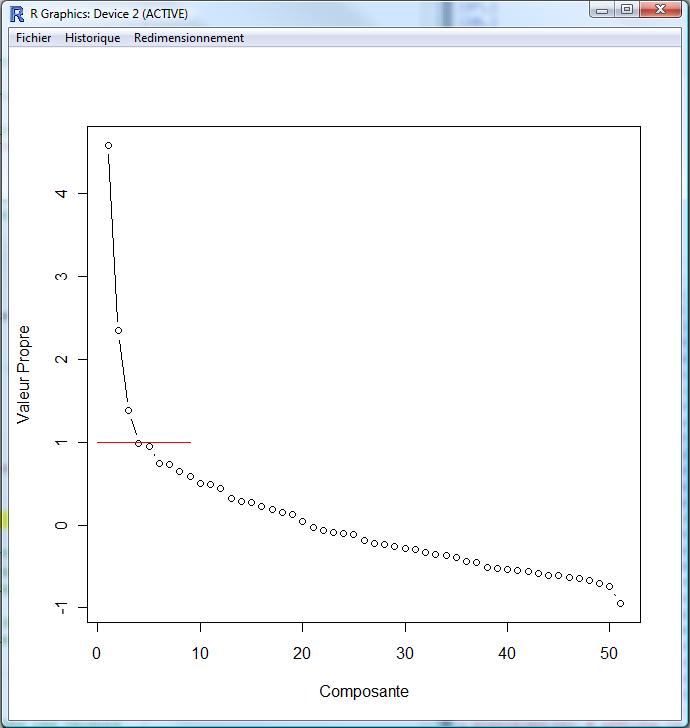
## Cependant, tous les cas, ne sont pas aussi simple. Une solution consiste à remplacer,
## dans la matrice de corrélation de la matrice de corrélations, la diagonale par les
## valeurs propres de la matrice CCX.
## Ensuite, on recalcule les valeurs propres de cette nouvelle matrice.
## On peut ensuite réaliser le graphique des valeurs propres.
Et maintenant le schéma résultant de cette seconde méthode.
###=========================================================================
## Certaines fonctions de l'environnement R nous permettent d'accélérer l'obtention des
## facteurs. La fonctions princomp() retourne l'analyse des composante.
## Pour apercevoir le contenu de notre matrice en enlevant les entrées trop petites
## il est possible de modifier la valeur de cutoff.
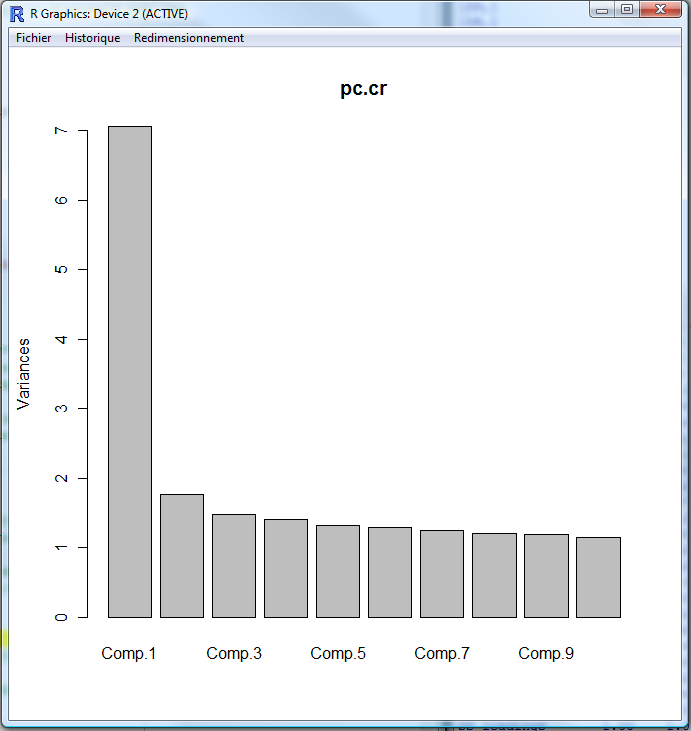
## La fonction plot(pc.cr) permet d'afficher le diagramme des éboulis.
## À partir de ce diagramme, il est possible d'extraire les facteurs en observant
## le changement dans la pente du graphique.
###================ Fin du script Section_09C_gamma.r ======================#
 Enregistrer sous...
Enregistrer sous...