

style1
Procédurier - Utiliser R en mesure et évaluation
Section 08 B - Analyse du PISA à partir de la théorie classique des tests
À la section 02 du procédurier (Section 02) nous avons calculé différents coefficients. Nous allons donc refaire ces calculs pour les éléments tirés du PISA. Plus spécifiquement, nous allons utiliser le fichier de données booklet9_01a.dat créé dans la partie A de la section 08.
Si vous n'avez pas le fichier booklet9_01a.dat Enregistrer sous...
Enregistrer sous...
Dans cette section, nous allons nous attarder aux questions mathématiques contenues dans le livret 9. Cependant, nous allons d'abord faire quelques opérations avec le fichier de données.
##############################################################################
## Fichier: Section_08B_alpha.r date: décembre 2007
## Auteur: AndréSèb Aubin (andreseb.aubin@gmail.com)
##
## Dans ce script
## Analyse de données du PISA selon la théorie classique des tests.
##
## Fichier initial de donnée: booklet9_01a.dat
##
## Alpha de Cronbach, Coefficient de Guttman (L2)
##
##############################################################################
##############################################################################
## 00 - Fonctions permettant d'initialiser l'environnement R
##############################################################################
rm(list=ls(all=TRUE))
library("grDevices")
setwd("C:/Documents and Settings/André-Sébastien/Mes documents/doctorat/TDII_Omega/Activite_finale/bin")
# setwd(choose.dir()) # À activer si on veut choisir le répertoire à chaque fois
# setwd("F:/PISA/bin") # Autre choix de répertoire (pour une clé USB par exemple)
##############################################################################
## 01 - Importation du fichier booklet9_01a.dat dans la matrice donnees_brutes
##############################################################################
donnees_brutes <- read.table(file="booklet9_01a.dat", header = TRUE)
Dimension <- dim(donnees_brutes)
Dimension
Cela nous donne les dimensions du fichier de données.
> Dimension
[1] 3315 73
Pour mieux comprendre comment les résultats complets des étudiants sont répartis, nous allons réaliser deux histogrammes: un premier avec tous les répondants et un second avec seulement ceux qui n'ont pas de NA dans leurs réponses.
##############################################################################
## 02 - Quelques manipulations sur les données
## Sur tous les étudiants ayant répondu au livret 09
###############################################################################
temp1 <- donnees_brutes[,6:70]
Sommes_etudiants <- rowSums(temp1, na.rm = TRUE)
paste("Moyenne = ", mean(Sommes_etudiants))
windowsize = 5
windows(width=windowsize, height=windowsize, restoreConsole = TRUE)
xname = Dimension[1]
hist(Sommes_etudiants, freq = TRUE, xlim=c(0,70), main = paste("Note totale de tous les " , xname, " candidats"),ylim = NULL, xlab = "Note", ylab="Fréquence des résultats (sur 1)")
fenetre = dev.cur()
## Nbre de candidats ayant des notes dans une fourchette définie
fourchette = c(30,35)
X <- subset(Sommes_etudiants, Sommes_etudiants > fourchette[1])
X <- subset(X, X < fourchette[2])
length(X)
## Sur les étudiants sans NA
Etudiant_sans_NA <- na.omit(donnees_brutes)
Nbre_etu <- dim(Etudiant_sans_NA)
temp <- Etudiant_sans_NA[,6:70]
Sommes_sans_NA <- rowSums(temp)
paste("Moyenne = ",mean(Sommes_sans_NA))
windows(width=windowsize, height=windowsize, restoreConsole = FALSE)
xname = Nbre_etu[1]
hist(Sommes_sans_NA, freq = TRUE, xlim=c(0,70), main = paste("Note totale des " , xname, " candidats"),ylim = NULL, xlab = "Note", ylab="Fréquence des résultats (sur 1)")
## Nbre de candidats ayant des notes dans une fourchette définie plus tôt
X <- subset(Sommes_sans_NA, Sommes_sans_NA > fourchette[1])
X <- subset(X, X < fourchette[2])
length(X)
Cela donne les graphiques suivants
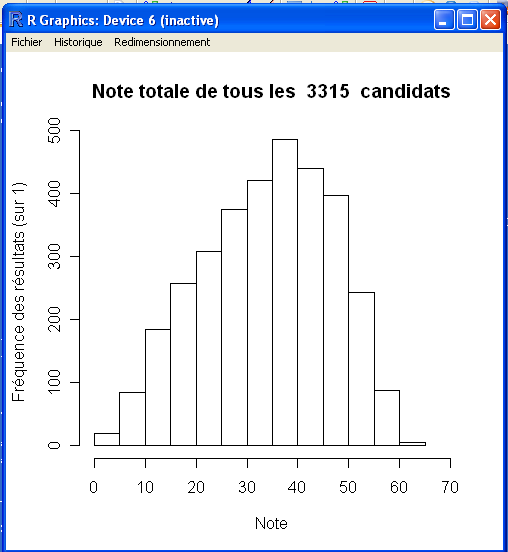
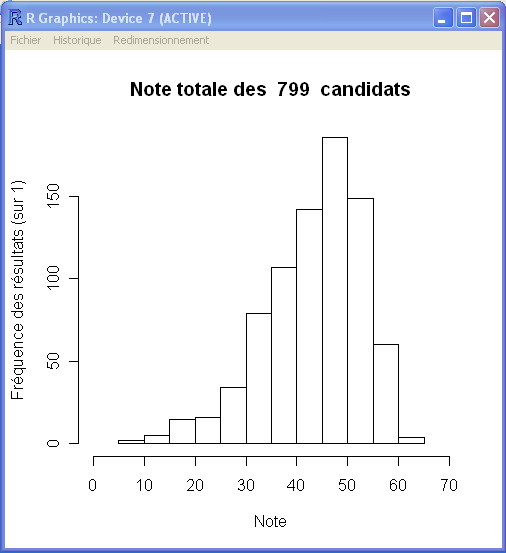
Nous allons maintenant extraire les questions du livret 9 touchant mathématiques et calculer l'alpha de Cronbach et le L2 de Guttman. Ces opérations sont les mêmes que celles décrites dans la section 03.
##############################################################################
## 03 - Extraction des questions mathématiques du livret 9
##
## Fichier de données initial: booklet9_01a.dat
## Fichier de sortie final: math_booklet9_01a.dat
##############################################################################
donnees_brutes <- read.table(file="booklet9_01a.dat", header = TRUE)
# Il est possible de tirer du CodeBook les questions du livret 09 les questions de mathématiques. La liste est placée dans une variable.
liste_question_math <- c("M033Q01", "M034Q01T", "M037Q01T", "M037Q02T", "M124Q01", "M124Q03T", "M144Q01T", "M144Q02T", "M144Q03", "M144Q04T", "M145Q01T", "M155Q01", "M155Q02T", "M155Q03T", "M155Q04T", "M192Q01T")
# On crée ensuite une matrice de données en extrayant des données complètes uniquement les questions de mathématiques
questions_math <- donnees_brutes[ ,liste_question_math]
questions_math[1:2,] # Cela ne change pas la matrice, mais affiche les 2 premières lignes.
write.table(questions_math, file="math_booklet9_01a.dat", row.names=FALSE, col.names=TRUE, sep="\t")
#colSums(questions_math) # ne fonctionne pas puisque la matrice comprend des NA
colSums(questions_math, na.rm = TRUE)
colMeans(questions_math, na.rm = TRUE)
dim_questions_math_omit <- dim(na.omit(questions_math))
dim_questions_math_omit # Nombre d'étudiants ayant répondu aux questions mathématiques.
##############################################################################
## 04 - Calculs de alpha et de L2
##
## Nous avons extrait une matrice de données qui ressemble à l'exercice
## fait à la section 02 (tableau 2.2)
##
## Inspiré du script tableau_2_7a.r
##
## Gestion des NA : Les répondants (lignes) contenant un NA ou plus sont
## omises pour le traitement.
##
## Matrice utilisée: questions_math sans NA
##
##############################################################################
questions_math_2 <- na.omit(questions_math)
questions_math_2[1:25,]
colSums(questions_math_2)
colMeans(questions_math_2)
## Calcul de l'alpha de Cronbach avec la fonction de R
cronbach(questions_math_2) # dans library(psy)
## Calcul de l'alpha de Cronbach avec le script fait à la main.
dim_questions_math_2 <- dim(questions_math_2)
nbre_item <- dim_questions_math_2[2]
nbre_item
nbre_individu <- dim_questions_math_2[1]
nbre_individu
colSums_questions_math_2 <- colSums(questions_math_2)
colSums_questions_math_2
rowSums_questions_math_2 <- rowSums(questions_math_2)
rowSums_questions_math_2
# Et la moyenne au test (fonction "mean()")
moyenne_questions_math_2 <- mean(rowSums_questions_math_2)
moyenne_questions_math_2
# Calculer la variance du test sX2_questions_math_2
sX2_questions_math_2 <- var(rowSums_questions_math_2)
# La variance calculée par "var()" est calculée en divisant par "n-1" et nous voulons
# la variance divisée par n, nous corrigeons en multipliant par "(n-1)/n" ou "15/16"
sX2_questions_math_2 <- sX2_questions_math_2*((nbre_individu - 1)/nbre_individu)
sX2_questions_math_2
cov_questions_math_2_a <- (cov(questions_math_2)*((nbre_individu - 1)/nbre_individu))
var_questions_math_2_a <- (var(questions_math_2)*((nbre_individu - 1)/nbre_individu))
for (i in 1:nbre_item) # mis à zéro de la diagonale
{
cov_questions_math_2_a[i,i] <- 0
var_questions_math_2_a[i,i] <- 0
}
var_questions_math_2_a # Covariance
cov_questions_math_2_a # Variance
sum(cov_questions_math_2_a)
sum(var_questions_math_2_a)
sum_si2 <- 0 # initialisation de la variable
for (i in 1:nbre_item)
{
sum_si2 = sum_si2 + ((colSums_questions_math_2[i] * (nbre_individu - colSums_questions_math_2[i])) / nbre_individu^2)
}
alpha <- ((nbre_item)/(nbre_item - 1))*(1 - (sum_si2 / sX2_questions_math_2))
sum_si2
alpha # Donne la même chose que l'autre méthode.
############################### Calcul de L2 ###################################
L2_questions_math_2_a <- c(0,0) # Initialisation
L2_questions_math_2_a[1] <- (sum(cov_questions_math_2_a))/(sX2_questions_math_2)
L2_questions_math_2_a[2] <- (sqrt((nbre_item)/(nbre_item - 1))) * (sqrt(sum(var_questions_math_2_a^2))/(sX2_questions_math_2))
sum(L2_questions_math_2_a) # Addition des deux termes de l'addition
> alpha # Donne la même chose que l'autre méthode.
M033Q01
0.6921613
>
> ############################### Calcul de L2 ###################################
>
> L2_questions_math_2_a <- c(0,0) # Initialisation
> L2_questions_math_2_a[1] <- (sum(cov_questions_math_2_a))/(sX2_questions_math_2)
> L2_questions_math_2_a[2] <- (sqrt((nbre_item)/(nbre_item - 1))) * (sqrt(sum(var_questions_math_2_a^2))/(sX2_questions_math_2))
>
> sum(L2_questions_math_2_a) # Addition des deux termes de l'addition
[1] 0.7014975
Il est étrange de constater qu'à la question M192Q01T, toutes les réponses (quand elles existent) sont 0. Voyons voir l'effet de cette question sur les coefficients.
################################################################################
##############################################################################
## 05 - Calculs de alpha et de L2 sans la question M192Q01T
##
## La question M192Q01T n'a aucune réponse à 1, elle ne discrimine donc pas.
## Voyons l'effet de son retrait
##
## Gestion des NA : Les répondants (lignes) contenant un NA ou plus sont
## omises pour le traitement.
##
## Matrice utilisée: questions_math sans NA (questions_math_2)
##
##############################################################################
questions_math_2b <- questions_math_2[,1:15]
questions_math_2b[1:25,] # Affichage des 25 premières lignes
colSums(questions_math_2b)
colMeans(questions_math_2b)
## Calcul de l'alpha de Cronbach avec la fonction de R
cronbach(questions_math_2b) # dans library(psy)
############################### Calcul de L2 ###################################
dim_questions_math_2b <- dim(questions_math_2b)
nbre_item2 <- dim_questions_math_2b[2]
nbre_item2
nbre_individu2 <- dim_questions_math_2b[1]
nbre_individu2
colSums_questions_math_2b <- colSums(questions_math_2b)
colSums_questions_math_2b
rowSums_questions_math_2b <- rowSums(questions_math_2b)
rowSums_questions_math_2b
# Et la moyenne au test (fonction "mean()")
moyenne_questions_math_2b <- mean(rowSums_questions_math_2b)
moyenne_questions_math_2b
# Calculer la variance du test sX2_questions_math_2
sX2_questions_math_2b <- var(rowSums_questions_math_2b)
# La variance calculée par "var()" est calculée en divisant par "n-1" et nous voulons
# la variance divisée par n, nous corrigeons en multipliant par "(n-1)/n" ou "15/16"
sX2_questions_math_2b <- sX2_questions_math_2b*((nbre_individu2 - 1)/nbre_individu2)
sX2_questions_math_2b
cov_questions_math_2b_a <- (cov(questions_math_2b)*((nbre_individu2 - 1)/nbre_individu2))
var_questions_math_2b_a <- (var(questions_math_2b)*((nbre_individu2 - 1)/nbre_individu2))
for (i in 1:nbre_item2) # mis à zéro de la diagonale
{
cov_questions_math_2b_a[i,i] <- 0
var_questions_math_2b_a[i,i] <- 0
}
var_questions_math_2b_a # Covariance
cov_questions_math_2b_a # Variance
L2_questions_math_2b_a <- c(0,0) # Initialisation
L2_questions_math_2b_a[1] <- (sum(cov_questions_math_2b_a))/(sX2_questions_math_2b)
L2_questions_math_2b_a[2] <- (sqrt((nbre_item2)/(nbre_item2 - 1))) * (sqrt(sum(var_questions_math_2b_a^2))/(sX2_questions_math_2b))
sum(L2_questions_math_2b_a) # Addition des deux termes de l'addition
################################################################################
####################### Fin du script Section_02A_alpha.r #####################
> cronbach(questions_math_2b) # dans library(psy)
$sample.size
[1] 1296
$number.of.items
[1] 15
$alpha
[1] 0.6952513
> sum(L2_questions_math_2b_a) # Addition des deux termes de l'addition
[1] 0.7016148
Les opérations qui viennent d'être présentées sont réunies dans le script suivant. Enregistrer sous...
Enregistrer sous...
Passons maintenant au coefficient de bissection, qui sont disponibles dans le script suivant. Enregistrer sous...
Enregistrer sous...
##############################################################################
## Fichier: Section_08B_beta.r date: décembre 2007
## Auteur: AndréSèb Aubin (andreseb.aubin@gmail.com)
##
## Dans ce script
## Analyse de données du PISA selon la théorie classique des tests.
##
## Fichier initial de donnée: math_booklet9_01a.dat (fait dans le script Section_02A_alpha.r)
##
## Coefficients de bissection
##
##############################################################################
##############################################################################
## 00 - Fonctions permettant d'initialiser l'environnement R
##############################################################################
rm(list=ls(all=TRUE))
library("grDevices")
setwd("C:/Documents and Settings/André-Sébastien/Mes documents/doctorat/TDII_Omega/Activite_finale/bin")
# setwd(choose.dir()) # À activer si on veut choisir le répertoire à chaque fois
# setwd("F:/PISA/bin") # Autre choix de répertoire (pour une clé USB par exemple)
##############################################################################
## 01 - Importation du fichier math_booklet9_01a.dat dans la matrice donnees_brutes
##############################################################################
questions_math <- read.table(file="math_booklet9_01a.dat", header = TRUE)
Dimension <- dim(questions_math)
Dimension
##############################################################################
## 02 - Calculs des coefficients de bissection
##
## Nous avons extrait une matrice de données qui ressemble à l'exercice
## fait à la section 03 (tableau 2.2)
##
## Inspiré du script tableau_2_7a.r
##
## Gestion des NA : Les répondants (lignes) contenant un NA ou plus sont
## omises pour le traitement.
##
## Matrice utilisée: questions_math sans NA
##
##############################################################################
questions_math_2 <- na.omit(questions_math)
questions_math_2[1:25,]
Dimension_2 <- dim(questions_math_2)
Dimension_2
nbre_individu <- Dimension_2[1]
nbre_individu
nbre_item <- Dimension_2[2]
nbre_item
# Premières opérations
# Additions des lignes pour valider la bonne saisie des données dans la matrice questions_math_2
# fonction "rowSums()"
# Cela donne le résultat du test de chaque sujet (étudiante ou étudiant)
rowsums_questions_math_2 <- rowSums(questions_math_2)
rowsums_questions_math_2
colsums_questions_math_2 <- colSums(questions_math_2)
colsums_questions_math_2
# Et la moyenne au test (fonction "mean()")
moyenne_questions_math_2 <- mean(questions_math_2)
moyenne_questions_math_2
# Faire deux matrices, chacune contenant la moitié des items.
y_1 <- matrix(0, nbre_individu, (nbre_item/2))
y_2 <- matrix(0, nbre_individu, (nbre_item/2))
# Même si cela est plus long et demandera un certain temps de compilation, par répartition aléatoire des items
nbre_iteration <- 10000 # Nombre d'itérations de la grande boucle.
rXX_G <- 0
rXX_G_Compil <- 0
rXX_SB_Compil <- 0
Compil <- matrix(0,nbre_iteration,(nbre_item+2))
for (m in 1:nbre_iteration) # Début de la grande boucle
{
h <- 1;
hasard <- 0
t <- as.integer(runif(1)*nbre_item+1)
hasard[h] <- t
h = h+1
OK <- 0
while (h != (nbre_item+1))
{
t <- as.integer(runif(1)*nbre_item+1)
hasard[h] <- t
for (h2 in 1:(h-1))
{
if (hasard[h] == hasard[h2])
{
OK <- 1
}
}
if (OK != 1)
{
h = h+1
}
OK <- 0
}
hasard
Compil[m,(1:nbre_item)] <- hasard[1:nbre_item]
y_1b <- matrix(0, nbre_individu, (nbre_item/2))
y_2b <- matrix(0, nbre_individu, (nbre_item/2))
for (k in 1:(nbre_item/2)) # Début de la petite boucle
{
y_1b[,k] <- questions_math_2[,hasard[k]]
y_2b[,k] <- questions_math_2[,hasard[k+(nbre_item/2)]]
} # Fin de la petite boucle
lignes.y_1b <- rowSums(y_1b)
lignes.y_2b <- rowSums(y_2b)
rYY <- (cor(lignes.y_1b,lignes.y_2b, method = "pearson"))
#rYY <- mean(lignes.rYY)
rYY
rXX_SB <- (2*rYY)/(1+rYY)
rXX_SB_Compil[m] <- rXX_SB
Compil[m,(nbre_item+1)] <- round(rXX_SB,3)
# Calculer la variance du test sX2
sX2 <- var(rowsums_questions_math_2)
# La variance calculée par "var()" est calculée en divisant par "n-1" et nous voulons
# la variance divisée par n, nous corrigeons en multipliant par "(n-1)/n" ou "15/16"
sX2 <- sX2*((nbre_individu - 1)/nbre_individu)
sX2 # variance corrigée
lignes.y_1b <- rowSums(y_1b)
lignes.y_2b <- rowSums(y_2b)
sY2_1b <- var(lignes.y_1b)
sY2_1b <- sY2_1b*((nbre_individu - 1)/nbre_individu)
sY2_1b # variance corrigée
sY2_2b <- var(lignes.y_2b)
sY2_2b <- sY2_2b*((nbre_individu - 1)/nbre_individu)
sY2_2b # variance corrigée
rXX_G <- 2*(1-((sY2_1b + sY2_2b)/sX2))
rXX_G_Compil[m] <- rXX_G
Compil[m,(nbre_item+2)] <- round(rXX_G,3)
} # Fin de la grande boucle.
# Maximum de rXX_SB
max(Compil[,(nbre_item+1)])
# Maximum de rXX_G
max(Compil[,(nbre_item+2)])
write.table(Compil, "math_booklet9_splithalf.data", row.names=F, col.names=F, sep=" ")
################################################################################
####################### Fin du script Section_02A_beta.r #####################
Cela donne donc les deux coefficients de bissection.
> # Maximum de rXX_SB
> max(Compil[,(nbre_item+1)])
[1] 0.748
>
> # Maximum de rXX_G
> max(Compil[,(nbre_item+2)])
[1] 0.748
>
> write.table(Compil, "math_booklet9_splithalf.data", row.names=F, col.names=F, sep=" ")
>
>
> ################################################################################
> ####################### Fin du script Section_08B_beta.r #####################
Pour accéder à la suite des manipulations de la section 08 Cliquez ici (Section_08_C).


 Enregistrer sous...
Enregistrer sous...

 Enregistrer sous...
Enregistrer sous... Enregistrer sous...
Enregistrer sous...